Lite Trans

Tag: Rumus

  • Rumus Volume Tabung: Contoh Soal, dan Penerapannya dalam Kehidupan Sehari-hari

    Tabung adalah salah satu bangun ruang yang sering dijumpai dalam matematika dan kehidupan sehari-hari. Memahami rumus volume tabung sangat penting untuk menyelesaikan berbagai masalah geometri, fisika, maupun aplikasi praktis. Artikel ini akan membahas secara komprehensif cara menghitung volume tabung, contoh soal, serta penerapannya dalam dunia nyata. Simak penjelasan lengkapnya di bawah ini!

    Apa Itu Tabung?

    Sebelum membahas rumus volume tabung, penting untuk memahami definisi dan ciri-ciri tabung. Tabung (atau silinder) adalah bangun ruang tiga dimensi yang terdiri dari dua lingkaran identik (alas dan tutup) serta sebuah selimut berbentuk persegi panjang yang melengkung. Ciri utama tabung adalah:

    1. Memiliki 2 sisi berbentuk lingkaran.
    2. Memiliki tinggi (t) yang merupakan jarak antara alas dan tutup.
    3. Tidak memiliki titik sudut.

    Tabung sering digunakan dalam kehidupan sehari-hari, seperti botol, pipa, drum, atau bahkan baterai. Kemampuan menghitung volume tabung menjadi kunci untuk menentukan kapasitas atau isi dari benda-benda tersebut.

    Rumus Volume Tabung

    Rumus Volume Tabung
    Rumus Volume Tabung

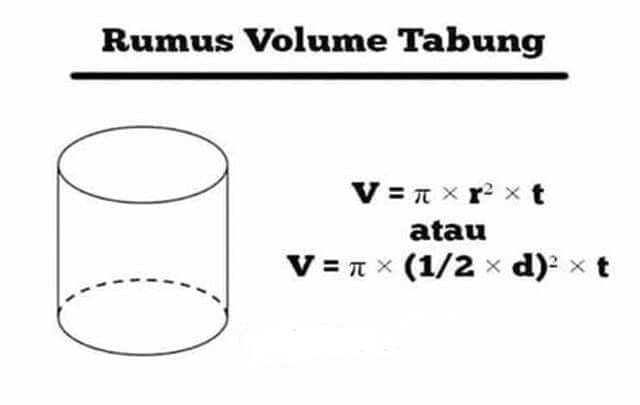
    Volume tabung dihitung dengan mengalikan luas alas (lingkaran) dengan tinggi tabung. Secara matematis, rumusnya adalah:

    Volume=π×r2×t

    Keterangan:

    • π (pi) ≈ 3,14 atau 22/7.
    • r = jari-jari alas tabung.
    • t = tinggi tabung.

    Contoh Penerapan Rumus:
    Jika sebuah tabung memiliki jari-jari 7 cm dan tinggi 15 cm, maka volumenya adalah:𝑉=22/7×72×15=2.310 cm3

    Langkah-Langkah Menghitung Volume Tabung

    Untuk memudahkan pemahaman, berikut langkah sistematis menghitung volume tabung:

    1. Tentukan jari-jari (r) dan tinggi (t). Pastikan satuan kedua nilai sama (misal, cm atau meter).
    2. Hitung luas alas tabung dengan rumus (πr2).
    3. Kalikan hasil luas alas dengan tinggi untuk mendapatkan volume.

    Tips:

    • Jika diketahui diameter (d), ubah ke jari-jari dengan rumus r = d/2.
    • Gunakan nilai π sesuai kebutuhan. Misal, jika jari-jari kelipatan 7, gunakan 22/7 untuk mempermudah perhitungan.

    Contoh Soal Volume Tabung dan Pembahasan

    Berikut contoh soal untuk melatih pemahaman tentang cara menghitung volume tabung:

    Contoh 1

    Sebuah tabung memiliki diameter 14 cm dan tinggi 10 cm. Berapakah volumenya?
    Penyelesaian:

    • Jari-jari (r = 14/2 = 7cm.
    • Volume = 22/7 x 72 x 10 = 1.549cm3.

    Contoh 2

    Drum minyak berbentuk tabung dengan volume 62.800 liter. Jika tingginya 200 cm, berapa jari-jari drum?
    Penyelesaian:

    • Konversi volume ke cm³: 62.800 liter = 62.800.000 cm³.
    • Rumus: (62.800.000 = 3,14 \times r2 x 200).
    • (r2 = 62.800.000/628 = 100.000.
    • (r = V100.000 = 316,23 cm.

    Baca Juga: Pengertian degree, radian, dan gradian

    Penerapan Volume Tabung dalam Kehidupan Sehari-Hari

    Menghitung rumus volume tabung tidak hanya berguna dalam matematika, tetapi juga dalam bidang teknik, industri, dan aktivitas sehari-hari. Berikut contoh penerapannya:

    1. Industri Manufaktur:
    • Menghitung kapasitas tangki bahan bakar, pipa, atau drum.
    • Merancang botol minuman agar sesuai dengan volume yang diinginkan.
    1. Pertanian:
    • Menentukan volume pupuk atau air dalam silo penyimpanan.
    1. Kesehatan:
    • Menghitung volume tabung oksigen medis untuk pasien.
    1. Rumah Tangga:
    • Mengukur kapasitas ember, termos, atau tabung gas LPG.

    Kesalahan Umum dalam Menghitung Volume Tabung

    Berikut kesalahan yang sering terjadi saat menggunakan rumus volume tabung dan cara menghindarinya:

    1. Mengabaikan Satuan:
    • Pastikan jari-jari dan tinggi dalam satuan yang sama sebelum dihitung.
    1. Keliru Menghitung Jari-Jari:
    • Jika diketahui diameter, jangan lupa dibagi 2 untuk mendapatkan jari-jari.
    1. Kesalahan Memilih Nilai π:
    • Gunakan 22/7 jika jari-jari atau diameter adalah kelipatan 7.
    1. Lupa Mengonversi Satuan Volume:
    • 1 liter = 1 dm³ = 1.000 cm³. Pastikan konversi satuan tepat.

    Baca Juga: Perkalian 1-10: Cara Mudah Menghafal dan Menguasai Matematika Dasar

    Fungsi dan Manfaat Memahami Rumus Volume Tabung

    Menguasai rumus matematika tabung memberikan manfaat luas, seperti:

    1. Meningkatkan Kemampuan Analitis:
    • Melatih logika dalam memecahkan masalah geometri.
    1. Membantu Perancangan Produk:
    • Penting dalam desain teknik dan arsitektur.
    1. Penghematan Biaya:
    • Menghitung volume material secara akurat menghindari pemborosan.

    Kesimpulan

    Rumus volume tabung (πr2t) adalah konsep dasar yang memiliki banyak aplikasi praktis. Dengan memahami langkah perhitungan, contoh soal, dan penerapannya, Anda dapat lebih mudah menyelesaikan masalah terkait volume silinder dalam berbagai konteks. Selalu perhatikan satuan, pilih nilai π yang tepat, dan hindari kesalahan umum untuk mendapatkan hasil akurat.

    FAQ (Pertanyaan Umum):

    1. Apa beda volume tabung dan luas permukaan tabung?
    • Volume mengukur kapasitas isi, sedangkan luas permukaan menghitung total area seluruh sisi tabung.
    1. Bagaimana cara mencari tinggi tabung jika diketahui volume dan jari-jari?
    • Gunakan rumus (t = V/πr2).
    1. Apakah rumus volume tabung sama dengan prisma?
    • Ya, karena tabung adalah prisma dengan alas lingkaran.

    Dengan menguasai rumus volume tabung, Anda dapat mengoptimalkan berbagai kegiatan sehari-hari yang melibatkan perhitungan kapasitas. Teruslah berlatih dengan contoh soal untuk meningkatkan pemahaman!

  • Rumus Luas Lingkaran: Pengertian, Cara Menghitung, dan Contoh Soal

    Lingkaran adalah salah satu bentuk bangun datar yang memiliki banyak aplikasi dalam kehidupan sehari-hari. Benda-benda seperti roda sepeda, jam dinding, setir mobil, dan uang koin adalah contoh bentuk lingkaran. Salah satu aspek penting dalam mempelajari lingkaran adalah cara menghitung luasnya menggunakan rumus luas lingkaran.

    Pada artikel ini, kita akan membahas secara mendalam tentang definisi lingkaran, ciri-ciri, bagian-bagian, hingga penerapan rumus luas lingkaran dalam berbagai contoh soal.

    Apa itu Lingkaran?

    Lingkaran adalah bangun datar dengan sisi melengkung yang membentuk sudut 360 derajat. Salah satu karakteristik utama lingkaran adalah jarak antara setiap titik pada kelilingnya dengan titik pusat selalu sama, yang disebut jari-jari atau radius.

    Ciri-Ciri Lingkaran

    Beberapa ciri-ciri lingkaran yang membedakannya dari bangun datar lainnya adalah:

    • Memiliki sudut 360 derajat.
    • Diameter membagi lingkaran menjadi dua bagian simetris.
    • Jari-jari adalah garis yang menghubungkan pusat lingkaran dengan kelilingnya.
    • Diameter selalu dua kali panjang jari-jari.

    Bagian-Bagian Lingkaran

    Luas Lingkaran

    Memahami bagian-bagian lingkaran penting sebelum mempelajari rumus luas lingkaran. Berikut adalah beberapa bagian utama lingkaran:

    1. Jari-jari (r): Jarak dari titik pusat ke keliling lingkaran.
    2. Diameter (d): Garis lurus yang melalui titik pusat dan ujung-ujungnya terletak di keliling lingkaran.
      • Rumus diameter: d=2×rd = 2 \times r
    3. Keliling Lingkaran (K): Panjang batas lingkaran yang dapat dihitung dengan rumus K=π×dK = \pi \times d.

    Baca Juga: Rumus Pythagoras: Dasar, Sejarah, dan Penerapannya

    Rumus Luas Lingkaran

    Rumus luas lingkaran digunakan untuk menghitung luas area yang ditempati lingkaran pada bidang dua dimensi. Rumus tersebut adalah: L=π×r×rL = \pi \times r \times r

    Keterangan:

    • LL: Luas lingkaran
    • π\pi: Konstanta dengan nilai 3,143,14 atau 227\frac{22}{7}
    • rr: Jari-jari lingkaran

    Contoh Soal Menggunakan Rumus Luas Lingkaran

    Berikut adalah beberapa contoh soal untuk memperjelas cara menghitung luas lingkaran:

    1. Contoh Soal Luas Lingkaran Penuh

    Sebuah roda memiliki jari-jari 14 cm. Hitunglah luas lingkaran tersebut.

    Diketahui:

    • Jari-jari (rr) = 14 cm

    Penyelesaian: L=π×r×rL = \pi \times r \times r L=227×14×14=616 cm2L = \frac{22}{7} \times 14 \times 14 = 616 \, \text{cm}^2

    Jadi, luas lingkaran adalah 616 cm².

    2. Contoh Soal Luas Lingkaran Berdasarkan Diameter

    Tali busur terpanjang sebuah lingkaran memiliki panjang 12 cm. Hitunglah luas lingkarannya.

    Diketahui:

    • Diameter (dd) = 12 cm
    • Jari-jari (rr) = d/2=12/2=6 cmd/2 = 12/2 = 6 \, \text{cm}

    Penyelesaian: L=π×r×rL = \pi \times r \times r L=227×6×6=113,14 cm2L = \frac{22}{7} \times 6 \times 6 = 113,14 \, \text{cm}^2

    Jadi, luas lingkaran adalah 113,14 cm².

    3. Rumus Luas Setengah Lingkaran

    Setengah lingkaran memiliki rumus: L=π×r×r2L = \frac{\pi \times r \times r}{2}

    Contoh Soal: Jari-jari lingkaran adalah 10 cm. Hitung luas setengah lingkarannya.

    Penyelesaian: L=3,14×10×102=157 cm2L = \frac{3,14 \times 10 \times 10}{2} = 157 \, \text{cm}^2

    Jadi, luas setengah lingkaran adalah 157 cm².

    4. Rumus Luas Seperempat Lingkaran

    Seperempat lingkaran memiliki rumus: L=π×r×r4L = \frac{\pi \times r \times r}{4}

    Contoh Soal: Lingkaran memiliki diameter 16 cm. Hitung luas seperempat lingkarannya.

    Penyelesaian:

    • Diameter (dd) = 16 cm
    • Jari-jari (rr) = d/2=8 cmd/2 = 8 \, \text{cm}

    L=3,14×8×84=50,24 cm2L = \frac{3,14 \times 8 \times 8}{4} = 50,24 \, \text{cm}^2

    Jadi, luas seperempat lingkaran adalah 50,24 cm².

    Baca Juga: Pengertian degree, radian, dan gradian

    FAQ Seputar Rumus Luas Lingkaran

    1. Apa itu π (pi)?
    Pi (π\pi) adalah konstanta matematis dengan nilai 3,143,14 atau 227\frac{22}{7}. Pi merepresentasikan perbandingan antara keliling lingkaran dan diameternya.

    2. Bagaimana menghitung luas lingkaran jika hanya diketahui diameter?
    Gunakan rumus jari-jari r=d/2r = d/2, lalu terapkan rumus L=π×r×rL = \pi \times r \times r.

    3. Apa perbedaan antara keliling dan luas lingkaran?
    Keliling lingkaran adalah panjang garis melingkar pada sisi luar lingkaran, sementara luas lingkaran adalah area yang ditempati lingkaran dalam bidang dua dimensi.

    Menghitung luas lingkaran menjadi lebih mudah jika kita memahami konsep dan rumusnya. Dengan menggunakan rumus luas lingkaran L=π×r×rL = \pi \times r \times r, Anda dapat menyelesaikan berbagai perhitungan luas lingkaran, setengah lingkaran, maupun seperempat lingkaran. Semoga artikel ini membantu Anda memahami dan menerapkan rumus luas lingkaran dengan baik.